Aluksi
Kultaisen leikkauksen geometrinen suhde – kokonaisuuden jako kahteen osaan niin, että pienempi osa suhtautuu suurempaan kuten suurempi kokonaisuuteen – on kiehtonut taiteilijoiden ja taiteentutkijoiden mieltä. Sen sanotaan olevan käyttökelpoinen suhde rakentamisessa ja visuaalisessa suunnittelussa; arkkitehdit operoivat sillä tai sen likiarvoilla, kuten suhdeluvuilla 3:5:8, jokapäiväisessä työssään. Näin myös entisaikain arkkitehtien ja kuvanveistäjien on uskottu tehneen. R. Herz-Fischler (1994, 1579–1584) mainitsee kuitenkin, että kreikkalaiset kiinnittivät tähän suhteeseen vain vähän huomiota ja että on väärin olettaa heidän suosineen sitä arkkitehtuurissa. Usein toistettu käsitys, että Luca Pacioli (Divina proportione, 1509) olisi puoltanut sen käyttöä taideteosten ja arkkitehtuurin suhteiden määrittelyssä, perustuu Herz-Fischlerin mukaan myös erehdykseen; Pacioli suositteli päinvastoin yksinkertaisia lukusuhteita. Italialaisten viulunrakentajien tiedetään sen sijaan käyttäneen Fibonaccin lukuja ohjenuoranaan 1600- ja 1700-luvulla.
Jos määrättyjen geometristen suhteiden käyttäminen kuvataiteen teosten, rakennusten ja käyttöesineitten suunnittelussa tuntuu luonnolliselta, niin jo paljon yllättävämpää on havaita, että myös säveltäjät operoivat samoilla suhteilla. Mitä voi tarkoittaa kultainen leikkaus jossakin musiikin muotorakenteessa? Musiikkihan etenee ajassa, ja ajan kokemukseen vaikuttavat monet satunnaiset tekijät, joita vaikea ennakoida ja hallita.
Joonas Kokkonen (1976) kertoo kuitenkin saaneensa Viimeisiä kiusauksia säveltäessään äkkiä oivalluksen, että ”toisen näytöksen on suhtauduttava ensimmäiseen kuten ensimmäinen näytös suhtautuu koko oopperaan”. Pekka Kuokkalan (1978) mukaan samaa suhdetta eri mittakaavoissa esiintyy oopperan rakenteissa muutenkin.
Kokkonen ei ole ainoa aikamme säveltäjä, joka on tietoisesti järjestänyt materiaaliaan ja suunnitellut muotorakenteitaan Fibonaccin lukujen pohjalla. Esim. Ernst Křenek, Karlheinz Stockhausen, Luigi Nono, Witold Lutosławski ja Per Nørgaard ovat kirjoittaneet teoksia, joissa Fibonaccin lukujen on annettu tarkasti määrätä musiikin eri parametrejä. Nämä teokset kuuluvat aikaan, jolloin eräänlainen uuspositivismi valtasi alaa säveltämistä koskevassa ajattelussa. Stockhausen julisti, että säveltämisen tulee olla samalla kertaa tutkimusta: säveltäjä asetti itselleen ongelman, ja teos oli sen ratkaisu.
Esiintyykö kultaisen leikkauksen käyttöä sitten aikaisemmassa musiikissa? Unkarilainen musiikintutkija Ernö Lendvai julkaisi 1957 artikkelin, jossa hän selittää, että kultainen leikkaus ja Fibonaccin luvut hallitsevat Bartókin musiikissa sekä harmoniaa ja melodiaa että muotoja. Kokkonen tutustui tähän artikkeliin ilmeisesti melko tuoreeltaan ja kokeili siinä esitettyjä ajatuksia Bartókin jousikvartettojen analyysiin. Hän pani merkille, että viidennessä kvartetossa kaksi viimeistä osaa suhtautuvat kolmeen ensimmäiseen kuten kolme ensimmäistä koko kvartettoon. Suhde on sama, jonka hän sittemmin toteutti Viimeisissä kiusauksissa.
Suomessa Jussi Jalas oli jo 1955 julkaissut kirjoituksen kultaisesta leikkauksesta Sibeliuksen sinfonioissa. Siinä hän tekee selkoa havainnoistaan, että Sibeliuksen sinfoniaosien väliset ja sisäiset kestosuhteet noudattavat kultaista leikkausta. Selvimmin näin on asian laita viidennessä sinfoniassa.
Sittemmin on asiaan palannut Olavi Kauko. Kirjoituksessaan ’Sibelius ja aika’ (Kauko 1981) hän julkaisee laskelmiaan viidennen sinfonian rakenteista. Jalas ja Kauko puhuvat kuitenkin eri asioista: kun Jalasta olivat kiinnostaneet kestosuhteet todellisessa esityksessä, Kauko sanoo ymmärtävänsä kultaisen leikkauksen ”muotoja tarkaan sääteleväksi lainalaisuudeksi”; hän ei mittaa reaaliaikaa, vaan laskee aika-arvoja käyttäen yksikkönä pienintä teoksessa esiintyvää rytmiyksikköä, kuudestoistaosaa.
Kokkonen on tarkastellut kultaisen leikkauksen toteutumista paitsi Bartókin kvartetoissa myös Mozartin pianosonaateissa. Hän kertoo panneensa Viimeisten kiusausten sävellystyön aikana ohimennen merkille, että kultainen leikkaus hallitsee Mozartin B-duuri-sonaatin (K.V. 570) ensimmäistä osaa. Myöhemmin hän kävi läpi Mozartin pianosonaattien kaikki sonaattimuotoiset osat ja kirjoitti havainnoistaan artikkelin ’Mozartin pianosonaatit ja sectio aurea’ (Kokkonen 1976). Siinä hän pyrkii osoittamaan, että ”Mozart ei ole kirjoittanut pianosonaateissaan ainoatakaan sonaattimuotoista osaa josta sectio aurea puuttuisi. Päinvastoin kultainen leikkaus esiintyy useimmiten monena eri kerroksena rakennetta kannattaen.”
Näyttää siis siltä, etteivät kultaisen leikkauksen suhteet ole musiikissa niinkään harvinaisia ja etteivät ne ole vain jollekin määrätylle aikakaudelle tai tyylille tunnusomaisia.
Jalas ja Kokkonen
Jalas ja Kokkonen korostavat kirjoituksissaan, että muusikkojen ja musiikin tutkijoiden olisi hyvä tuntea kultaisen leikkauksen käsite. Jos esimerkiksi muotojen rajakohdat ovat moniselitteiset, kultaisen leikkauksen suhde saattaa Jalaksen mukaan tarjota ”lopullisen ratkaisun” ongelmaan. Kokkonen on samalla kannalla. Jos sivuteeman paikantaminen klassisessa sonaattiosassa on hankalaa tai mahdotonta, silloin kultaisen leikkauksen suhde saattaa ”paljastaa meille tarkasti, missä tuo kiistelty sivuteema sijaitsee”. Kultainen leikkaus on eräänlainen deus ex machina, joka tuo ratkaisun kun muita keinoja ei enää ole.
Yleisempiäkin etuja kultaisen leikkauksen suhteiden tarkkailulla voidaan saavuttaa. Jalaksen mukaan se voi ”antaa vastauksen säveltaiteen ydinkysymyksiin”, ”selventää mutojen tajuamista” ja luoda ”pohjaa musikaaliselle ajattelulle, joka helposti joutuu hämärien spekulaatioiden tielle”. Luovat taiteilijat voivat kultaisen leikkauksen valossa ”tarkastella luomiensa muotojen kestävyyttä” ja esittäjät tarkistaa tempojaan. Jos suhteet noudattavat kultaista leikkausta, silloin säveltäjä voi luottaa muotojensa lujuuteen ja esittäjä pitää tempojaan onnistuneina; muuten on syytä huoleen, ehkä perusteellisiin tarkistuksiin. Kokkonenkin uskoo esittäjän hyötyvän kultaisen leikkauksen käsitteestä. Säveltäjälle sillä sen sijaan on arvoa vain ehdollisesti; sävellyksen rakennehan ”ei hevin voi syntyä mittaamalla ja laskemalla. Jos lähtökohta on tämä – eikä mittatikku – silloin tietoisuus kultaisen leikkauksen olemassaolosta voi olla hyvinkin hedelmällinen.”
Niin vakuuttunut kuin Kokkonen onkin kultaisen leikkauksen merkityksestä musiikissa, hänen suhteensa siihen on oudon jakaantunut. Tietoinen konstruoiminen on jollakin tavoin epäilyttävää ja tuomittavaa, mutta jos säveltäjä luo kultaisen leikkauksen suhteita intuitiivisesti, on tämä vain osoitus siitä, että hänellä on vaistomainen oikeiden suhteiden taju – että hänellä on ”musiikilliset suhteet jäsenissään”, kuten Andreas Werckmeister sanoi aikalaisestaan Johann Sebastian Bachista. Jalas puolestaan on vakuuttunut siitä, ettei Sibelius ”suinkaan ole etukäteen matemaattisella kaavalla laskenut rakenteittensa lujuutta. Niiden intuitiivinen lainalaisuus kuitenkin näyttää, miten luonnonmukaisesti ja kuinka syvällä luomisprosessi on tapahtunut.” Kultainen leikkaus ei ole vain matemaattinen kaava, se on kappale luontoa ja elämää. Toisaalta Jalas kuitenkin mainitsee Sibeliuksen itsensä joskus viitanneen ’kultaiseen jakoon’ musiikissaan ”tosin sen tarkemmin selittämättä tai perustelematta tätä nähtävästi intuitiivista lausettaan”. Tällä viittauksella perimätietoon Jalas nähtävästi haluaa antaa omalle tulkinnalleen arvovaltaa ja uskottavuutta. Mutta sittenkin hänen on pakko kommentissaan selittää Sibeliuksen lausumaksi kerrottu huomautus intuitiiviseksi; muutenhan säveltäjän ylle saattaisi langeta epäilys, että hänen musiikkinsa onkin konstruoitua eikä – niinkuin sen tulee olla – syntynyt hänen neroudestaan luonnollisen kasvuprosessin tuloksena.
Zeising
Kultaiselle leikkaukselle on vuosituhansien aikana kertynyt kosolti arvovaltaa. Se herättää mielikuvan täydellisestä, ehkä saavuttamattomasta kauneudesta, joka on ihmisen kaipuun ja hellittämättömän pyrkimyksen kohde. Taiteen tutkijat ovat pyrkineet todistamaan, että juuri tämä matemaattinen suhde ilmeisesti oli se kaanon, joka antiikin Kreikan klassisella kaudella oli sekä kuvanveistossa että arkkitehtuurissa osien ja kokonaisuuden välisten suhteiden perustana (Tatarkiewicz 1970, 72). Myöhempinä aikoina siihen on palattu yleensä silloin, kun antiikin esikuvan mukainen puhdaslinjainen, sopusointuinen taide on koettu kauneuden korkeimmaksi ihanteeksi.
1800-luvun estetiikassa kultaisen leikkauksen kultin herätti henkiin Adolf Zeising. Zeisingille kauneuden korkein ihanne on ihminen, joka sekä henkensä että ruumiinrakenteensa puolesta on täydellisin kaikista olioista. Niinpä kauneuden ideaa voidaan parhaiten tutkia tutkimalla ihmisruumiissa vallitsevia suhteita. Tälle tehtävälle Zeising omistautuu teoksessaan Neue Lehre von den Proportionen des menschlichen Körpers, joka ilmestyi 1854, samana vuonna kuin Eduard Hanslickin essee Vom Musikalisch-Schönen. Teoksensa loppuluvuissa Zeising laajentaa näkökulmaansa myös mm. arkkitehtuuriin ja musiikkiin.
Zeising uskoi löytäneensä kultaisessa leikkauksessa sekä luonnossa että taiteessa yleisesti pätevän esteettisen periaatteen. Hänen mukaansa ei tosin pidä odottaa, että todelliset ilmiöt milloinkaan vastaisivat täydellisesti yleistä lakia, sillä jokainen yksityinen ilmiö on sellaisenaan väistämättä jossakin määrin epätäydellinen. Lakia on pidettävä kaikkialla pikemminkin ideaalityyppinä tai normaalisuhteena, jota todelliset ilmiöt enemmän tai vähemmän lähestyvät.
Zeising käsittää siis kultaisen leikkauksen platoniseksi ideaksi, mutta hänen näkemyksensä poikkeaa Platonin ideaopista kuitenkin siinä tärkeässä suhteessa, ettei hän pidä todellisten ilmiöitten epätäydellisyyttä puutteena, vaan pikemminkin täydellisyyden mielikuvan edellytyksenä. Täydellisimpiä ilmiöitä eivät suinkaan ole ne, jotka toteuttavat lain ”koko sen ankaruudessa ja jäykkyydessä”, vaan päinvastoin ne, joilla ”niinkuin ihmisruumiilla on hallussaan sisäisen elämän ja itsemääräämisen koko voima”; poikkeamat ihanteesta eivät kumoa lakia, vaan panevat sen liikkeeseen ja ilmentävät sitä korkeammalla ja vapaammalla tavalla.
Zeising oli puhdas formalisti. Hän oli vakuuttunut siitä, että kauneuden ilmiö perustuu oikeisiin suhteisiin osien kesken ja osien ja kokonaisuuden välillä. Niinpä hän torjui Kantin käsityksen, että tarkoituksenmukaisuudella olisi jotakin tekemistä kauneuden kanssa; sillä tarkoituksenmukaisuus on toki jotakin aivan muuta kuin suhteellisuus. Tätä ajatustaan Zeising perustelee hämähäkkiesimerkillä. Kukaan ei kiellä, hän sanoo, etteikö hämähäkki olisi ”erittäin tarkoituksenmukaisesti varustettu sitä tehtävää varten, joka sillä näyttää olevan…; mutta että sen pitkien ohuiden jalkojen ja paksun pallomaisen ruumiin välillä olisi laatuunkäypä mittasuhde, sitä tuskin kukaan uskaltaa väittää, eivät edes ne, jotka kauneuden määritelmälleen mieliksi ovat kyllin rohkeita selittämään hämähäkit kauniiksi” (Zeising 1854, 8).
Musiikin estetiikassa kultainen leikkaus ei ole koskaan saanut yhtä tukevaa jalansijaa kuin kuvataiteen teoriassa ja kauneuden filosofiassa, jota Zeising ensi sijassa edusti. Zeising kuitenkin uskoi, että hänen löytämänsä Proportionalgesetz pätee yhtä hyvin akustisissa kuin optisissakin ilmiöissä. Hän katsoi kreikkalaisten filosofien olleen oikeilla jäljillä, kun he johtivat musiikin teorian perusteet matematiikasta; mutta kreikkalaiset eivät löytäneen musiikin teorialle yhtenäistä selitysperustaa, jollaista täytyy pitää tyydyttävän teorian edellytyksenä, vaan johtivat ilmiöt kahdesta erilaisesta suhdejärjestelmästä, toisaalta aritmeettisesta ja toisaalta harmonisesta sarjasta.
Zeising kritikoi erityisesti pythagoralaista konsonanssiteoriaa. Hän ei hyväksynyt ajatusta, että intervallien kauneus olisi riippuvainen sen sävelten värähdyslukusuhteitten yksinkertaisuudesta, mistä olisi seurauksena, että oktaavi olisi täydellisin intervalli. Oktaavi ei ”tosin millään tavalla loukkaa korvaa, mutta siinä ei myöskään ole mitään erityisen miellyttävää”. Sen sävelten värähdysluvut melkein sulautuvat toisiinsa, niin että kuulija luulee kuulevansa yhden ainoan sävelen. Tämä intervalli siis tyydyttää mitä suurimmassa määrin yhtenäisyyden tarvetta, mutta vain hyvin puutteellisesti kauneuden toista periaatetta, moninaisuuden vaatimusta; vaikka sitä ei koetakaan epämiellyttäväksi, niin se on kuitenkin karu ja tyhjä, ja niinpä sitä käytetäänkin musiikissa vain perussävelvaikutelman tehostamiseen. ”Sen tähden se ei missään tapauksessa voi olla kaunein ja täydellisin kaikista konsonansseista.”
Muutkaan yksinkertaisiin lukusuhteisiin perustuvat intervallit eivät saa Zeisingin hyväksymistä. Kvintti suorastaan loukkaa korvaa, kvartti on luonteeltaan labiili, terssi ei muodosta suljettua, rauhallista kokonaisuutta; mikään niistä ei ole niin tyydyttävä, että sitä voitaisiin käyttää sävellyksen päätöksenä. Täysin tyydyttävää konsonanssia on siis etsittävä pikemminkin sellaisten intervallien joukosta, joiden värähdyslukusuhteet ovat mutkikkaampia ja joita perinteellisessä teoriassa ei ole pidetty edes itsenäisinä intervalleina, vaan tällaisista intervalleista johdettuina. Näin ollen on mahdotonta, että periaate, jonka varaan konsonanssiteoria on rakennettu, voisi olla oikea.
Tämä ristiriita on tiedostettu teoriassa itsessäänkin, Zeising huomauttaa, ja siitä on seurauksena lause, ettei kahden sävelen yhdistelmä ylipäätäänkään voi tuottaa täyttä tyydytystä; todelliseen harmoniaan tarvitaan vielä kolmas sävel. Tällä tavoin teorian perustaksi tulee kolmisointu. Sointuteorian lähtökohta, että kahden osatekijän yhdistelmä (Zweiheit) on sellaisenaan riittämätön esteettisen vaikutelman aikaansaamiseksi, on periaatteessa oikea; lisäksi tarvitaan yhdentävä tekijä. Mutta yhdentäminen ei voi tapahtua sillä tavoin, että kahden eritasoisen sävelen muodostamaan intervalliin lisätään uusi kolmas tekijä, vaan ainoastaan siten, että nämä kaksi säveltä sulautetaan uudeksi korkeammaksi ykseydeksi tai kolmiyhteydeksi. ”Todella kolmiyhteisessä konsonanssissa ei sen tähden suinkaan tarvita kolmea eri säveltä, vaan alkuperäisessä muodossaan se toteutuu pikemminkin jo yhdistämällä toisiinsa kaksi säveltä, joiden tulee olla toisiinsa sellaisessa suhteessa, että ykseyden ja kakseuden, identiteetin ja erilaisuuden periaate tulee todella sovitetuksi.” Tämän ehdon täyttää Zeisingin mukaan ainoastaan sama suhde, joka on sekä ihmisruumiin että ylipäätään näkyvien ilmiöiden muodollisen kauneuden perustana: kultainen leikkaus.
Suhde voidaan ilmaista kokonaisluvuilla 3, 5, 8 ja 13. Yhtälöä 3:5 = 5:8 vastaavat sävelsuhteet es:c = e:es+c ja yhtälöä 5:8 = 8:13 sävelsuhteet e:c = c:e+c. Näissä soinnuissa on vain kaksi elementtiä, sävelet es ja c tai e ja c, mutta niiden lisäksi niissä esiintyy perussävelen oktaavikerrannainen. Sen suhde perussävelen terssiin on seksti, joka käytännössä on tunnustettu täydellisimmäksi konsonanssiksi mutta joka teoriassa on jäänyt varjoon, koska lähtököhtana on pidetty sitä virheellistä periaatetta, että pelkästään lukusuhteiden yksinkertaisuus ratkaisee konsonanssin arvon. Edellä esitettyjä sävelyhtälöitä hallitsee sama periaate kuin ihmisruumiin suhteita. ”Oktaavin yhdistäminen perussävelen suuren terssin kanssa vastaa siis yläruumiin ja alaruumiin suhdetta miehen hahmossa, oktaavin yhdistäminen pienen terssin kanssa puolestaan yläruumiin ja alaruumiin suhdetta naisen hahmossa; edelliselle on näin ollen luonteenomaista suurempi ankaruus ja kovuus ja siksi sitä kutsutaan duurisoinnuksi; jälkimmäiselle taas on luonteenomaista suurempi taipuisuus ja pehmeys ja sitä kutsutaan mollisoinnuksi.”
Saatuaan päätökseen todistelunsa, että seksti on täydellisin kaikista konsonansseista, Zeising johtaa tonaalisen musiikin perustana olevat kolmi- ja nelisoinnut sekstiprogressiosta ja päätyy toteamukseen, että sävelten esteettinen vaikutus perustuu samalla tavoin kuin näkyvien ilmiöidenkin suhteellisuuden alkulakiin (Urgesetz der Proportionalität), joka on kultaisen leikkauksen idea. Kultainen leikkaus on ”luovan voiman sisimmässä salaa vaikuttava hahmotusperiaate”, joka säätelee ja järjestää kaiken niin taiteessa kuin luonnossakin – ja taiteessa yhtä usein tiedottomasti kuin luonnossakin. Mutta missä tämä periaate halutaan tuhota ja missä sitä pilkataan, sieltä on myös turha etsiä kauneutta – ainakaan muodon kauneutta. (Zeising 1854, 423–444.)
Fechner, Lipps ja Birkhoff
Filosofina Zeising oli idealisti: hän tarkasteli todellisuutta yleisten ideoiden ja käsitteiden valossa. Kauneus oli hänelle muodon kauneutta, ja muodon kauneus perustui oikeisiin suhteisiin osien ja kokonaisuuden välillä. Jo 1800-luvun loppupuolella Zeisingin uusplatonilainen näkemys kohtasi ankaraa vastustusta. Gustav Theodor Fechner (1876) kutsui sitä von Oben herab -estetiikaksi ja halusi asettaa sen tilalle kokeellisen psykologisen tutkimustavan, joka etenee päinvastoin yksityisestä yleiseen, von Unten herauf. Esteettisten ”normaalisuhteitten” konstruoiminen oli hänen mielestään filosofisesti epäilyttävää, ja hän luetteli suuren joukon heikkouksia, joita yleisistä ideoista lähtevään tutkimukseen tavallisesti sisältyy. Tällaisessa tutkimuksessa nojaudutaan liiaksi perusteettomiin teoreettisiin esikäsityksiin, ei tehdä kyllin selvää eroa assosiatiivisen ja välittömän mielihyvän välillä, annetaan liian suuri merkitys välittömän mielihyvän yksityistapauksiin liittyville ehdoille, otetaan kokemusperäisten tosiasioiden tarkastelussa huomioon vain teoreettista lähtökohtaa tukevat tapaukset, käytetään liian monimutkaisia esimerkkejä (kuten ihmisruumis), joissa erilaiset mielihyvän kokemiseen vaikuttavat tekijät sekoittuvat toisiinsa, lyödään laimin pyrkiä yksinkertaisuuteen koejärjestelyissä virheiden välttämiseksi. Nämä Zeisingin metodiin kohdistetut moitteet sisältävät suurimman osan empiirisen tieteen piirissä esitetyn idealismin kritiikin argumenteista.
Mutta Fechner ei tyytynyt pelkästään metodikritiikkiin, vaan teki myös sarjan kokeita testatakseen Zeisingin väitteitä. Hän suunnitteli empiirisen koejärjestelyn saadakseen selville, millaisia muotoja ihmiset todella pitävät kauniina. Kokeiden tulokset osoittivat mm., että kultaista leikkausta noudattavat tai tätä suhdetta likellä olevat suorakaiteet todella koetaan muita miellyttävämmiksi. Toisaalta horisontaalisen janan jakaminen kultaisen leikkauksen suhteessa on ratkaisevasti epätyydyttävämpi kuin sen tasajako. Ristissä miellyttävin pysty- ja poikkipalkin välinen suhde taas on 2:l. Näiden tulosten perusteella Fechner katsoo Zeisingin liioitelleen kultaisen leikkauksen esteettistä arvoa. Hän ei kuitenkaan kokonaan sitä kiistänyt. Tämän askeleen otti Theodor Lipps (1914). Hän ei tosin asettanut kyseenalaiseksi kultaista leikkausta noudattavan suorakaiteen miellyttävyyttä, mutta kylläkin sen johtopäätöksen, että tämä miellyttävyys johtuisi kultaisesta leikkauksesta. Lipps kirjoittaa: ”Nyttemmin voidaan pitää yleisesti hyväksyttynä – ja tämä olisi oikeastaan pitänyt alun perinkin käsittää –, että kultainen leikkaus on ylipäätään, kuten tässäkin tapauksessa, esteettisesti täysin merkityksetön, ettei missään tämän suhteen toteutuminen perustele minkäänlaista mielihyvää.” Mielihyvän aiheuttavat suhteiden selväpiirteisyys ja sopusuhtaisuus, mutta nämä ominaisuudet ovat tunnusomaisia myös monille muille kuin kultaisen leikkauksen suhteille. Sen sijaan esimerkiksi suorakaide, joka muistuttaa neliötä mutta ei ole neliö, koetaan epämiellyttäväksi epämääräisyytensä takia. (Lipps 1914, 66.) Lippsin kannalle asettuu myös George Birkhoff (1933, 27–39), joka muistuttaa siitä, että Platonin suosiman suorakaiteen sivujen suhdeluku oli 1.732. Tämä suhde on yhtä selväpiirteinen kuin kultainen leikkauskin. Birkhoff arvostelee myös Fechnerin kokeita, joissa hänen mielestään ei ole otettu huomioon kaikkia tulokseen vaikuttavia tekijöitä.
Lippsin ja Birkhoffin kantaa voidaan pitää myös nykyisen estetiikan näkemyksenä. Enää ei uskota, että mikään puhtaasti formaalinen kriteeri ainakaan yksin voisi perustella kauneuden ilmiön. Monroe C. Beardsleyn (1958, 508) mukaan ”olisi mitä mieluisinta, jos jokin tämänkaltainen yksinkertainen kaava voisi mitata kauneuden havaitsemisen ehdot. Mutta nähdäkseni tähän mennessä ei ole kovinkaan luotettavasti osoitettu, että kultainen leikkaus tai mikään yksinkertainen ideaalisten suhteiden joukko olisi enempää kauneuden välttämätön kuin riittäväkään ehto.”
Lendvai
Musiikinteoriassa kultaisen leikkauksen idea on kaikesta huolimatta vielä ajankohtainen aihe. Tämä johtunee mm. Ernö Lendvain Bartók-tutkimusten (Lendvai 1957, 1983, 1993) nauttimasta arvovallasta. Lendvain teorian mukaan Bartókin musiikin harmonia- ja muotoperiaatteet perustuvat kultaiseen leikkaukseen ja Fibonaccin lukuihin. Nämä suhteet ovat siinä yhtä tärkeä muotoelementti kuin symmetriset säkeet ja periodit tai yläsävelsarjaan perustuva soinnutus wieniläisklassisessa musiikissa.
Lendvai selittää ensinnäkin, että Fibonaccin luvut hallitsevat Bartókin kromaattista järjestelmää. Jos intervallien laajuus ilmoitetaan niiden sisältämien puolisävelaskelten lukumäärinä, voidaan todeta, että monissa Bartókin teemoissa hallitsevia intervalleja ovat suuri 2 (suuri sekunti), 3 (pieni terssi), 5 (puhdas kvartti), 8 (pieni seksti) ja 13 (ylinouseva oktaavi). Sama lukusarja on määräävä tekijä myös sointurakenteissa. Kromaattisessa ympäristössä esiintyvä mollikolmisointu on kvarttisekstisoinnun (8 = 5+3) ja duurikolmisointu sekstisoinnun (8 = 3+5) muodossa. Kun nämä soinnut yhdistetään, saadaan Bartókille tunnusomainen duuri-molli-sointu, johon usein liittyy vielä septimi. Lendvai ristii tämän soinnun α-soinnuksi ja toteaa sen esiintyvän Bartókin musiikissa yhtä usein kuin dominanttiseptimisointu esiintyy klassisessa tyylissä.
Todisteen siitä, että kultainen leikkaus kuuluu ”musiikin sisimpiin lakeihin”, Lendvai näkee pentatoniikassa, ”ihmiskunnan kenties vanhimmassa säveljärjestelmässä”, jota hän pitää kultaisen leikkauksen puhtaimpana musiikillisena ilmenemismuotona; tämän säveljärjestelmän tunnusomaiset intervallit ovat nimittäin suuri sekunti (2), pieni terssi (3) ja puhdas kvartti (5), kaikki ”Fibonacci-intervalleja”. Myös edellä mainittu α-sointu voidaan johtaa pentatoniikasta, mikä puolestaan osoittaa, että pentatoniikalla ja kromatiikalla on Bartókin musiikissa likeinen yhteys. (Lendvai 1957, 116–117.)
Kultaiseen leikkaukseen perustuvat edelleen Bartókin paljon käyttämät sointumallit 1:5 (pieniä sekunteja ja puhtaita kvartteja), 1:3 (pieniä sekunteja ja terssejä) sekä 1:2 (pieniä ja suuria sekunteja). Ne suhtautuvat toisiinsa, kuten 5:3:2. Tärkein malleista on 1:2. Siihen perustuvaa asteikkoa c-cis-e-fis-g-a-b Lendvai kutsuu Bartókin kromaattisen järjestelmän ”toonika-asteikoksi” ja mainitsee, että sen avulla voidaan ratkaista hänen mutkikkaimpienkin melodioittensa ja sointujensa tonaalisuus. Varsinainen ”kultaisen leikkauksen sävelrivi” on kuitenkin asteikko, jossa perussävelen ja joidenkin asteiden välillä esiintyy Fibonaccin lukuja noudattavia intervallisuhteita. Tämän asteikon, esim. c-d-es-f-ges-as-b, Fibonacci-intervallit ovat pieni terssi (3), puhdas kvartti (5) ja pieni seksti (8). Bartókin diatoninen järjestelmä, jonka tunnusomainen asteikko on ”akustinen sävelrivi”, esim. c-d-e-fis-g-a-b, puolestaan on kultaisen leikkauksen lakien ”systemaattinen käännös”. (Lendvai 1957, 118–137.)
Lendvain tulkintaa Bartókin kromaattisen järjestelmän Fibonacci-perustasta on arvostellut Jonathan Kramer (1973), joka pitää sen havaitsemista Fibonacci-rakenteeksi epätodennäköisenä. ”Bartók on saattanut johtaa tämänkaltaiset säveltasorakenteet samasta sarjasta, jota hän joskus käytti kestosuhteissa, mutta tämä yhtäläisyys on pohjimmiltaan merkityksetön. Sitä ei voida havaita eikä sen seurauksia voida havaita, etenkään koska säveltasorakenteissa käytetään vain Fibonacci-arvoja 1, 2, 3, 5 ja joskus 8. Lendvain esimerkit kuullaan todennäköisemmin tyylillisenä pyrkimyksenä välttää intervallia 4 (suuri terssi) kuin Fibonacci-intervallien 1, 2, 3 ja 5 yhdistelminä.” Kramer myöntää kuitenkin, että niissä harvoissa tapauksissa, joissa sarjaan sisältyy myös intervalli 8 (pieni seksti), kultaisen leikkauksen hahmottaminen on todennäköisempää. Tämäkin johtopäätös tuntuu liialliselta myönnytykseltä. Se edellyttäisi, että intervallit kuultaisiin puoliaskelten summina ja intervallisuhteet puoliaskelten summien aritmeettisina suhteina. Tämä vaikuttaa sangen vähän uskottavalta. Hahmopsykologian valossa näyttää pikemminkin siltä, että intervallit hahmotetaan itsenäisinä olioina, joilla on kullakin oma musiikillinen ja musiikillisen perinteen välittämä luonteensa. Havaittuina ilmiöinä ne eivät ole enempää puoliaskeleista koostuvia pilareita kuin värähdyslukujen suhteitakaan.
Tältä pohjalta lähtee myös Hermann Pfrognerin (1963) Lendvain asteikkotermeihin kohdistama kritiikki. Pfrogner korostaa, että nimitys ”akustinen asteikko” painottaa liian suoraan ja yksioikoisesti tämän sävelasteikon sukulaisuutta yläsävelsarjan kanssa. Ajatus, että sen sävelet olisi johdettu yläsävelsarjasta, voi johtaa fysikalistisiin väärinkäsityksiin, sillä sävelasteikko ei lopultakaan ole akustinen vaan musiikillinen tosiasia. Termin ”kultaisen leikkauksen sävelrivi” Pfrogner torjuu kokonaan. Kun nämä kaksi asteikkoa (esim. 1) ovat rakenteeltaan samankaltaisia (jälkimmäinen on edellisen käännös), on ensinnäkin ristiriitaista sanoa, kuten Lendvai tekee, että toinen edustaa Bartókin diatonista ja toinen kromaattista maailmaa. Toiseksi Bartókin ”peiliasteikossa”, kuten Pfrogner sitä nimittää, esiintyy myös vähennetty kvintti, jonka sisältämä puoliaskelten lukumäärä (6) ei sovi Fibonaccin lukusarjaan. Tähän voidaan lisätä, että samoin on pienen septimin (10) laita. Edelleen Pfrogner mainitsee, että tärkeä Fibonaccin lukusarjan jäsen 13 sattuisi sävelelle des tai cis, joka ei kuulu asteikkoon. Lendvain termi ”akustinen asteikko” perustuu näin ollen tulkintaan, joka ei ota huomioon kaikkia säveliä. Samoin perustein on myös Peter Petersen (1971, 11–12) arvostellut Lendvain tapaa johtaa duuri-molli-sointu ja eräät muut soinnut Fibonaccin luvuista. Lendvain väite, että kultaisen leikkauksen systeemi selittäisi Bartókin harmonian, ei ole oikeutettu, hän huomauttaa.
Kultaisen leikkauksen suhteista Bartókin muotorakenteissa Lendvai antaa myös useita esimerkkejä. Bartókin sonaattimuotoisissa osissa on tavallista, että kertauksen alku sattuu tarkalleen kultaisen leikkauksen kohdalle, ja muuntyyppisissä osissa kultainen leikkaus osoittaa usein huippukohdan. Sama suhde hallitsee myös pienempiä muotoyksikköjä, kuten 16:tta johdantotahtia Sonaatissa kahdelle pianolle ja lyömäsoittimille, tai suurempia, kuten samaa teosta kokonaisuudessaan: kultainen leikkaus osuu siinä 1/8:n tarkkuudella ensimmäisen ja toisen osan rajalle. (Lendvai 1957, 103–108.)
Ensimmäinen ja kolmas osa teoksessa Musiikkia kielisoittimille, lyömäsoittimille ja celestalle rakentuvat Lendvain (1957, 104–105) mukaan kokonaisuudessaan kultaisen leikkauksen suhteille. Ensimmäisen osan huippukohta jakaa osan 89 tahtia (tahteja on partituurissa oikeastaan 88, mutta Lendvain mukaan osan jälkeinen tauko voidaan laskea 89. tahdiksi) suhteessa 55 + 34 tahtia. Edellinen jakso jakaantuu soinnillisesti kahteen osaan edelleen samassa suhteessa: 34 ensimmäistä tahtia soitetaan con sordino, 21 seuraavaa senza sordino. Huippukohdan jälkeinen jakso puolestaan jakaantuu samalla tavoin suhteessa 13 + 21 tahtia. Edelleen Lendvai toteaa, että ekspositio päättyy tahdissa 21 ja että viimeiset 21 tahtia jakaantuvat suhteessa 13+8. Kaikki mainitut luvut kuuluvat Fibonaccin lukusarjaan.
Nämä tulokset vaikuttavat pikaisesti katsottuina vakuuttavilta. Kun niitä tutkii lähemmin, havaitsee pientä vilppiä. Laskelmat heittävät tahdin siellä, toisen täällä. Jonathan Kramer (1973, 120–121) on huomauttanut, että huippukohta saavutetaan tahdissa 56 (55 tahdin jälkeen), kun taas sordinot poistetaan ja lyömäsoittimet tulevat sisään tahdissa 34 (33 tahdin jälkeen). Kumpaa laskutapaa sitten sovelletaankin, aina muodostuu yhden tahdin ero. Myös tahdissa 78 tapahtuu huomattava tekstuurin muutos, jota korostaa celestan sisääntulo, ”mutta se puuttuu Lendvain kaaviosta, ehkä siksi ettei se sovi hänen analyysiinsa”. Tällä kohden mieleen palautuu Fechnerin kritiikki Zeisingin metodista: huomioon otetaan vain teoreettista lähtökohtaa tukevat seikat. Vakavampi huomautus on kuitenkin se, että Lendvai laskee tahteja, vaikka tahtilaji vaihtelee jatkuvasti; ja tässä tyylissä ”kirjoitettu tahti ei ole selvästi kuultavissa yksikkönä”. Samoin hän menettelee analysoidessaan teoksen kolmatta osaa, jonka sisäiset suhteet noudattavat Fibonaccin lukusarjaa, kun lasketaan 4/4-tahteja ja katsotaan välillä esiintyvät 3/2-tahdit puolentoista tahdin arvoisiksi. Osassa esiintyy kuitenkin, kuten Kramer huomauttaa, myös 5/4- ja 2/4-tahteja, joita Lendvai ei ota millään tavalla huomioon. Lendvai menettelee tässä itse lausumansa periaatteen vastaisesti: analysoidessaan Bartókin Divertimenton ensimmäistä osaa hän nimenomaan huomauttaa käyttävänsä laskennallisena yksikkönä triolia, koska ”tahtilajin vaihtumisen johdosta tahtien lukumäärä ei ole ratkaiseva”.
Lendvai on aivan hiukan kaunistellut todellisuutta saadakseen esiin puhtaan Fibonaccin lukusarjan. On vaikea ymmärtää, miksi tämä on ollut tarpeellista. Edes Zeising ei vaatinut, että todelliset ilmiöt vastaisivat jäännöksettömästi yleistä lakia. Vähäiset epätarkkuudet Lendvain laskelmissa herättävät kuitenkin periaatteellisen kysymyksen: miten suuria poikkeamia säännöstä yleensä voidaan sallia, ennen kuin kultaisen leikkauksen suhde on kokonaan menetetty? Tähän kysymykseen ei yksikään kultaisen leikkauksen teoreetikoista ole vastannut.
Mielenkiintoinen ja valaiseva esimerkki kultaisen leikkauksen problematiikan monitahoisuudesta Bartókin musiikissa on Allegro barbaron tapaus. Tässä pianokappaleessa teemaryhmien välillä esiintyy tahteja, joiden ainoa musiikillinen sisältö on fis-molli-soinnun rytmikäs vasarointi. Niiden tehtävänä on erottaa teemaryhmät selvästi toisistaan. Lendvai (1957, 104) on kiinnittänyt huomiota siihen, että näiden ostinato-jaksojen laajuus on milloin 8, milloin taas 5, 3 tai 13 tahtia; hän pitää tätä tapausta vaikuttavana esimerkkinä Fibonaccin lukusarjan käytöstä. Myös Kramer hyväksyy tämän esimerkin ja tekee sen yhteydessä kaksi tärkeää periaatteellista huomautusta. Hän toteaa, että Fibonacci-ryhmät ovat jokaisen parametrin suhteen sisäisesti eriytymättömiä. ”Tämä on tärkeää sen tähden, ettemme tule jakaneeksi näitä kestoja edelleen osiin, jotka eivät noudata Fibonacci-suhteita, ja koska Fibonacci-tahtien staattisuus sekä erottaa ne kappaleen muista jaksoista että myös tekee sarjan additiivisen luonteen selvästi havaittavaksi. Sillä jotta Fibonaccin lukusarjan additiivisella luonteella olisi mitään merkitystä, läsnä tulee olla vähintään neljä perättäistä jäsentä. […] 8 yksikköä sisältävän keston kuuleminen 5 ja 3 yksikköä sisältävien kestojen summaksi ei ole erikoisasemassa: pienemmät kestot olisivat yhtä hyvin voineet olla esimerkiksi 6 ja 2. Mutta kun Bartók panee peliin neljännen Fibonacci-keston (13), joka kuullaan edeltäneiden 8 ja 5 yksikköä sisältäneiden kestojen summana, huomaamme systeemin eleganssin ja ekonomian. Näin ollen 13-tahtinen fis-molli-sointu ei ole tyydyttävä niinkään sen tähden, että se laajentaa Fibonaccin systeemiä yhdellä jäsenellä, vaan siksi, että se todella vasta määrittelee systeemin.” (Kramer 1973, 118–119.)
Nuottien tarkastelun perusteella näyttää siis siltä, että Allegro barbaron ostinato-jaksot olisivat erityisen vakuuttava ja todistusvoimainen esimerkki Lendvain teorian puolesta. Bartókin vuodelta 1929 peräisin oleva äänitys tästä teoksesta saattaa asian kuitenkin kokonaan uuteen valoon. László Somfai (1981) on nimittäin pannut merkille, että tahtien lukumäärä tässä äänityksessä poikkeaa kolmessa kohdassa Universal Editionin julkaisemasta nuottipainoksesta. Kaikissa tapauksissa kysymyksessä ovat juuri teemojen väliset ostinato-tahtiryhmät. Tahdeissa 50–57 Bartók soittaa kahdeksan tahdin asemasta vain kuusi, tahdeissa 88–100 kolmentoista tahdin sijasta kaksitoista ja tahdeissa 144–149 viiden tahdin sijasta seitsemän. Nämä muutokset merkitsevät elegantin Fibonacci-rakenteen täydellistä tuhoutumista. Millainen lähdearvo sitten on Bartókin äänityksellä? Sehän on vain teoksen yksittäinen esitys, kun taas nuottijulkaisu edustaa teosta itseään. Somfai pitää kuitenkin äänitettä teoksen tärkeänä primaarilähteenä myös tekstikriittiseltä kannalta. Bartók soitti Allegro barbaroa säännöllisesti konserteissaan, ja näissä esityksissä teos vielä julkaisemisensa jälkeen hioutui ja sai tarkemman muodon. Somfai esittää myös musiikillisesti järkeviä perusteita Bartókin tekemille muutoksille.
Szentkirályi, Bachmann ja Bachmann
Lendvain teoria on esittänyt merkittävää osaa Bartók-reseptiossa. Lendvai on itse tehnyt sitä tunnetuksi kirjoituksissa ja kirjoissa, joita on julkaistu paitsi unkariksi myös saksaksi ja englanniksi (Lendvai 1957, 1960, 1971, 1983, 1993). Hänen tutkimuksiaan on myös referoitu erilaisille kohderyhmille. Esimerkiksi Edward Lowman (1971) on tehnyt niistä selkoa Fibonacci Quarterlyn lukijoille. Lendvain ajatuksia on myös sovellettu uusien esimerkkitapausten analyysiin, ja niissä on saatu hänen teoriaansa vahvistavia tuloksia.
Lendvain teorian näyttää varauksettomasti hyväksyvän András Szentkirályi (1978), joka on tarkastellut Bartókin sävellystekniikkaa toisen viulusonaatin kahdessakymmenessä alkutahdissa. Hän pyrkii osoittamaan, samoin kuin Lendvai edellä mainitussa analyysissaan alkutahdeista Sonaatissa kahdelle pianolle ja lyömäsoittimille, että tämän jakso muotorakenne noudattaa kultaisen leikkauksen suhteita. Itse asiassa hän esittää vielä paljon voimakkaamman väitteen: ”Sonaatin koko muotorakenne kehkeytyy viulun äänen mikrostruktuurista kolmessa ja puolessa johdantotahdissa.” Tätä väitettä on kuitenkin mahdotonta tutkia, koska Szentkirályi ei osoita, miten tuo kehkeytyminen tapahtuu. Sen sijaan on hyödyllistä tarkastella hänen analyysiaan mainituista johdantotahdeista. Nämä tahdit, joissa viulu toistaa kaksiviivaista e-säveltä, sisältävät tahdin 4 fermaattiin asti, mutta sitä lukuunottamatta, 21 1/8-yksikköä, jotka jakaantuvat seuraavasti:
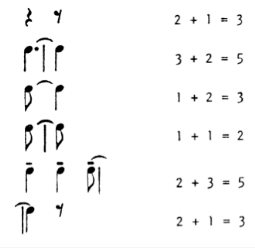
Kuva 1
Rakenteessa voidaan erottaa kaksi puoliskoa, joiden kestot ovat 11 ja 10 1/8-yksikköä. Rajakohdassa, joka on merkitty dim. calando, äänenvoimakkuus ja ilme muuttuvat. Jälkimmäisen puoliskon sävelet on myös yhdistetty säekaarella. Tässä jaksossa esiintyy myös sisäisiä rajakohtia: kahden ensimmäisen 1/8-yksikön jälkeen sointiväri vaihtuu, kun siirrytään e-kieleltä d-kielelle, ja samasta pisteestä alkaen sävelet soitetaan tenuto (pidättäen, siten että niiden koko aika-arvo pääsee ilmoille). Uusi äänenvoimakkuuden muutos (pp) sattuu jakson viimeiselle neljäsosalle.

Kuva 2
Szentkirályi on pyrkinyt tarkkaan huomioimaan struktuuria eriyttäviä tekijöitä, joiden hän näkee jäsentävän sitä Fibonaccin lukujen suhteessa. Toisaalta hän jättää ottamatta huomioon sellaisia tekijöitä, jotka eivät sovi tähän kuvaan. Epäselvää on ensinnäkin, millä perusteella rakenteeseen luetaan kuuluvaksi tahdin 4 kolmannen tahtiosan 1/8-tauko, mutta ei seuraavaa, fermaatilla varustettua taukoa, johon säkeen täytyy ymmärtää päättyvän. Toiseksi hän ei ota huomioon uutta tempomerkintää poco rall., joka hidastaa tempoa tahdin 3 toiselta tahtiosalta alkaen ja pidentää kahdeksasosien kestoa säkeen loppupuolella. Kolmanneksi rytmiyksikköjen ryhmitys noudattaa samasta pisteestä alkaen eri periaatetta kuin aikaisemmin: Szentkirályi irrottaa tahdin 3 viimeisen 1/8-yksikön tahdin 4 ensimmäisen tahtiosan 1/4-yksiköstä, johon se on sidottu kaarella, ja yhdistää sen edeltävään 1/4-yksikköön. Jäljelle jäävän 1/4-yksikön hän puolestaan sitoo sitä seuraavaan taukoon. Nämä operaatiot ovat mielivaltaisia; niiden avulla on ilmeisesti pyritty väkisin tuottamaan Fibonaccin lukujen mukaisia ryhmityksiä (2 + 3 = 5 ja 2 + 1 = 3), joista nuotinnettu rakenne (2 + 2 = 4 ja 3 + 1 = 4) poikkeaa.
Kokonaan toinen kysymys on se, miten kuulija hahmottaa edellä kuvatut tahdit. Niiden kesto on Joseph Szigetin ja Bartókin omassa esityksessä n. 15 sekuntia, jolloin 1/8-yksikön kesto on keskimäärin 0,7 sekuntia. Ei ole todennäköistä, että kuulija laskee tällaisia kestoja yhteen havaitakseen, että niiden suhteet noudattavat Fibonaccin lukuja.
Nuotinnettu rakennekin noudattaa kuitenkin musiikillista logiikkaa, joka on erilainen kuin Fibobaccin lukujen matemaattinen logiikka. Ensinnäkin viulun e”-sävelen kesto on jokaisella toistokerralla erilainen, ja näistä kestoista muodostuu kiilamainen, ensin lyhenevä ja sitten pitenevä sarja: 5, 3, 2, 2+, 2++, 3+++, jossa +-merkki ilmaisee tempon hidastumisesta aiheutuvaa 1/8-yksikön keston pitenemistä. Toiseksi atakkien metrinen asema vaihtuu jatkuvasti. Näiden keinojen avulla Bartók on luonut vaikutelman vapaasta rytmistä, joka on irronnut tahtilajin orjuudesta. Sen kanssa Fibonaccin luvuilla ei ole mitään tekemistä.
Puhuessasaan sonaatin ensimmäisen osan teeman kokonaismuodosta Szentkirályi siirtyy käyttämään laskennallisena yksikkönä kahdeksasosan asemasta tahtia. Kun neljän tahdin mittainen teema jakaantuu 1 1/2:n ja 2 1/2:n tahdin mittaisiin säkeisiin, Szentkirályi näkee niiden rajakohdassa kultaisen leikkauksen. Kahdeksasosissa laskettuna säkeet ovat kuitenkin lähes samanmittaiset (17/8 ja 18/8), sillä ensinnäkin tahtilaji vaihtuu siten, että jälkimmäiseen säkeeseen sisältyy yksi muita lyhyempi tahti (9/8+9/8+6/8+9/8), toiseksi edelliseen säkeeseen on luettava kohotahti (2/8) ja kolmanneksi ensimmäinen säe kattaa 2/3 eli (6/8) eikä puolet toisesta tahdista. Jos on sallittua vaihdella laskutapaa aina sen mukaan, miten odostusten mukainen tulos parhaiten saadaan ja jos pituuksia ja kestoja on lupa arvioida summittaisesti silmämitalla, kultaisen leikkauksen suhteita on toki helppo löytää mistä tahansa rakenteesta.
Szentkirályi yrittää perustella menettelyään väittämällä, että Bartókin partituureissa tahtiviivat eivät jaa aikaa mekaanisesti, vaan osoittavat korostuksia; ja kun korostukset eivät välttämättä seuraa toisiaan säännöllisin välein, tahdit eivät myöskään ole samanmittaisia, mikä ei tarkoita, että ne lakkaisivat toimimasta perustavina aikayksikköinä. Päättely kiertää kehää ja ajautuu ristiriitaan. Vaihtuvat tahtilajit kuuluvat olennaisesti vapaaseen rytmiin, jossa säännöllistä iskutusta pyritään välttämään. Tässä sonaatissa Bartókin tahdit nimenomaan ovat pelkästään laskennallisia yksikköjä, jotka eivät osoita korostuksia; tämä on helppo havaita jo siitäkin, että puheena olevassa jaksossa jokaisen tahdin (paitsi ensimmäisen) ensimmäinen tahtiosa sidotaan edeltävän tahdin viimeiseen, mikä eliminoi systemaattisesti tahdin pääiskun.
Myös Bachmann ja Bachmann (1979) kannattavat Lendvain teoriaa ja selittävät, että Bartókin musiikki rakentuu kultaiselle leikkaukselle ja on niiden funktio. Mutta heidänkään laskutoimituksensa eivät ole moitteettomia. Heidän mukaansa Bartókin Contrasts-trion ’Sebes’-osan più mosso -taite (tahdit 132–168) on kokonaisuudessaan mainittujen suhteiden hallitsema. Tahtilaji todella noudattaa Fibonaccin lukuja, sillä se on merkitty 8+5/8. 1/8-yksikköjä on tahdissa yhteensä 13, ja tahdin osatkin on jaettu lukusarjan edellyttämällä tavalla (8 = 3+2+3 tai 1+2+2+2+1 ja 5 = 2+3 tai 2+2+l). Mutta lisäksi Bachmann ja Bachmann yrittävät todistaa, että taitteen rakennekin noudattaa Fibonaccin lukuja. Heidän argumenttinsa perustuu toteamukseen, että 1/8-yksikköjen rytmitys tahdin sisällä vaihtuu tahdissa 148 ja että taitteen jälkimmäinen jakso tästä tahdista loppuun (t. 168) käsittää 21 tahtia. Jotta tällä seikalla olisi merkitystä, più mosson kokonaiskeston pitäisi olla 34 tahtia ja edellisen puoliskon 13 tahtia; tällöin muodostuisi Fibonaccin lukusarjan mukaisia suhteita. Mutta todellisuudessa nämä luvut ovat 37 ja 16.
Toinen Bachmannin ja Bachmannin esimerkki koskee Bartókin toisen viulukonserton finaalin tahteja 213–214. He esittävät näistä tahdeista harmonisen analyysin, joka perustuu Lendvain akseliteorialle, ja kiinnittävät huomiota siihen, että ainoa akselien ulkopuolinen sävel as tahdin 214 alussa (kuva 3) sattuu kultaisen leikkauksen kohdalle, sillä se on kymmenes kaikkiaan 16 sävelestä. Tämä tulkinta sivuuttaa sen tosiasian, että tahdin 214 viimeinen sävel f on kestoltaan samanarvoinen triolien kanssa, joten kultainen leikkaus – mikäli sen laskeminen tällaisesta katkelmasta ylipäätäänkään on mielekästä – ei suinkaan satu as-sävelelle. Toiseksi: mainitut tahdit eivät sisällä 16 1/8-yksikköä, kuten diagrammissa esitetään, vaan 12; onhan tahtilaji 3/4.

Kuva 3
Vakuuttavimman Fibonacci-rakenteen Bachmann ja Bachman ilmoittavat löytäneensä Bartókin Musiikkia kielisoittimille, lyömäsoittimille ja celestalle -teoksen ensimmäisen osan lopputahdeista (kuva 4). He laskevat tahtien sisältävän 25 1/8-yksikköä ja toteavat, että kultainen leikkaus (0.618 x 25 = 15.45) osuu 15. ja 16. yksikön väliselle tahtiviivalle, pisteeseen jossa molemmat johtosävelet purkautuvat a-toonikaan. On kuitenkin absurdia sanoa leikkauksen sattuvan tahtiviivalle; tosiasiassa se sattuu tämän laskutavan mukaan katkelman toisen tahdin viimeisen kahdeksasosan puolivälin tienoille. Bachmannilta ja Bachmannilta on myös jäänyt huomaamatta, että heidän esimerkkinsä viimeisessä tahdissa on painovirhe; kun tahtilaji on 11/8 tulisi päättävän neljäsosan perässä olla joko piste tai 1/8-tauko, jolloin 1/8-yksikköjen lukumäärä lisääntyy yhdellä. Kun se otetaan huomioon laskuissa, kultainen leikkaus (0.618 x 26 = 16.068) sattuukin viimeisen tahdin ensimmäiselle tahtiosalle, ei kuitenkaan aivan sen alkuun. Tämä sijainti saattaisi antaa jopa enemmän painoa kultaisen leikkauksen rakenteelliselle merkitykselle puheena olevassa katkelmassa kuin Bachmannin ja Bachmannin epätarkkaan lukemiseen perustuva väkinäinen yritys nähdä merkitystä siinä, että tahtiviiva osoittaa leikkauksen paikan. Mutta tämänkin jälkeen voidaan kysyä, mikä oikeuttaa jättämään katkelman ensimmäisen tahdin alussa oleva 1/4-tauon huomiotta; sisältyyhän sekin rakenteeseen. Näin ollen yksikköjä onkin lopulta 28, ja kultainen leikkaus (0.618 x 28 = 17.304) sattuu jälleen katkelman toisen tahdin viimeiselle kahdeksasosalle, suunnilleen samalle kohdalle, mihin se myös Bachmannin ja Bachmannin virheellisen laskutavan mukaan sijoittuu. Kokonaan epäselväksi jää kuitenkin, mitä kultaisen leikkauksen sijainnilla tämän esimerkin yhteydessä halutaan todistaa. Musiikillisesti merkityksellinen ja merkitykselliseksi hahmottuva tosiasia on johtosävelen purkautuminen toonikaan, ei tämän purkautumisen geometrinen sijainti kontekstistaan irroitetussa katkelmassa. Mistä tahansa kolmen tahdin jaksosta voidaan helposti laskea kultainen leikkaus; ja sen jälkeen tarvitaan vain hiven käsitteellistä akrobatiaa sen selittämiseksi, miksi on merkityksellistä, että kultainen leikkaus sattuu juuri siihen mihin se sattuu.

Kuva 4
Bachmann ja Bachmann lukevat samoista tahdeista vielä muitakin merkittävinä pitämiään suhteita. Käänteinen kultainen leikkaus (esimerkissä rG.S.) sattuu heidän mukaansa huippukohtaan, es-sävelelle, joka Lendvain akseliteoriassa on toonikan vastapooli. Tässäkin kirjoittajalle on sattunut kömmähdys: mainitulle sävelelle sattuu katkelman kahden ensimmäisen tahdin käänteinen kultainen leikkaus (0.382 x 15 = 5.73), jos alussa oleva 1/4-tauko jätetään pois laskuista, kuten Bachmann ja Bachmann tekevät. Koko katkelman käänteinen kultainen leikkaus (0.382 x 25 = 9.55 Bachmannin ja Bachmannin premissien mukaan, 0.382 x 28 = 10.696 edellä selostetut virheet korjattuina) sen sijaan ei osu mihinkään rakenteellisesti tärkeään pisteeseen.
Fibonaccin lukusarjan Bachmann ja Bachmann löytävät katkelmasta myös seuraavasti: he esittävät, että sen rytmirakenne noudattaa es-sävelestä alkaen Fibonaccin lukuja 3, 5, 8 ja 21. Kun edellä mainittu painovirhe otetaan huomioon, viimeinen näistä luvuista ei pidä paikkaansa. Sitä paitsi lukusarja katkeaa, sillä viimeisen tahdin ensimmäinen tahtiosa ei ole 13. vaan 12. kahdeksasosa. Kramer on huomauttanut, että lukusarjan hahmottaminen edellyttää vähintään neljän peräkkäisen termin läsnäoloa. Tämä ehto ei mainitussa tapauksessa toteudu.
Kaiken kaikkiaan on todettava, että Bachmannin ja Bachmannin analyysit sisältävät niin runsaasti virheitä ja epäjohdonmukaisuuksia, ettei niitä voi ottaa vakavasti. Ne osoittavat Fechnerin olleen oikeassa, kun hän arvosteli von Oben herab -estetiikkaa taipumuksesta ottaa huomioon vain teoreettista lähtökohtaa tukevat tosiasiat ja laiminlyödä sitä vastaan puhuvat.
Lowman, Chailley ja Werner
Kritiikki, jota Kramer, Pfrogner ja Petersen ovat esittäneet Lendvain teorioita vastaan, on pääasiassa metodista laatua. He ovat osoittaneet Lendvain ottaneen huomioon vain sellaisia tosiasioita, jotka tukevat hänen perusolettamustaan, ja sivuuttaneen toisia, jotka ovat tämän olettamuksen kanssa ristiriidassa. Kramerin kanta ei kuitenkaan ole kokonaan torjuva. Hän katsoo, että Lendvai on pohjimmiltaan oikeassa selittäessään Bartókin käyttäneen kultaista leikkausta ja Fibonaccin lukuja rakenteellisina periaatteilla musiikissaan; nämä periaatteet eivät vain ole niin yleispäteviä ja merkitseviä kuin Lendvai haluaisi. Kramer toisin sanoen uskoo, että kultainen leikkaus ja Fibonaccin luvut joissakin tapauksissa sisältyvät Bartókin musiikin ”intentionaaliseen rakenteeseen”. Samaan käsitykseen viittaavia ilmaisuja sisältyy, kuten olemme todenneet, paitsi Lendvain omiin myös Szentkirályin sekä Bachmannin ja Bachmannin kirjoituksiin. Voimakkaimmin tämän kannan ovat ilmaisseet Bachmann ja Bachmann: ”Näin ollen Béla Bartókin musiikissa on lukuisia esimerkkejä siitä, että kultaista leikkausta ja Fibonaccin lukusarjoja on käytetty rakenteen perustana. Niiden käyttö ei rajoitu vain lyhyisiin katkemiin hänen musiikissaan; kokonaisia kappaleita on konstruoitu näiden uusien taiteellisten keinojen avulla. On päätettävä, että Bartókin musiikki on rakennettu kultaisille leikkauksille ja Fibonaccin luvuille ja on niiden suoranainen funktio…”
Lowman on päätelmissään varovaisempi. Hän toteaa, että Bartók on saattanut tuntea matemaattista mielenkiintoa kultaiseen leikkaukseen tai hän on saattanut löytää Fibonaccin luvut etsiessään tietoisesti muita kuin kahden kertaluvuille perustuvia hahmoja musiikillisille ideoilleen. Mutta todennäköisempää on, että hänen tekniikkansa kasvoi esiin musiikillisten ideoiden hahmoista itsestään.
Myös Chailley (1966) torjuu päättäväisesti ajatuksen, että Bartókilla olisi sävellystyössään ollut jokin teoreettinen lähtökohta. Mielikuva Bartókista, joka laskee kappaleensa pituudeksi 563 trioliyksikköä ja kertoo tämän luvun 0.618:lla saadakseen selville, että hänen tulee aloittaa kertaus 348. trioliyksiköllä, on hänen mielestään epätodennäköinen ja ristiriidassa sen kanssa mitä hänestä tiedämme. Bartók on itsekin halunnut antaa sävellystyöstään kuvan, joka näyttää vahvistavan Chailleyn epäluuloja. Harvard-luennoissaan hän mainitsee, ettei koskaan luonut uusia teorioita etukäteen. ”Vihasin sellaisia ajatuksia. Minulla oli tietenkin hyvin selvä mielikuva määrätyistä suunnista, joihin halusin edetä, mutta työskennellessäni en kiinnittänyt mitään huomiota määritelmiin, jotka soveltuisivat näihin suuntiin tai niiden lähteisiin. Tämä asenne ei tarkoita, että olisin säveltänyt ilman […] tarkkoja suunnitelmia ja ilman riittävää kontrollia. Suunnitelmat koskivat uuden teoksen henkeä ja teknisiä ongelmia (esimerkiksi teoksen hengen edellyttämää muodollista rakennetta), jotka kaikki tiedostin enemmän tai vähemmän vaistomaisesti, mutta en koskaan askarrellut yleisten teorioiden kanssa soveltaakseni niitä teoksiin, jotka aioin kirjoittaa.” (Bartók 1976, 376.) Tämä huomautus sisältyy Harvard-luennoissa jaksoon, jossa Bartók kuvaa kromatiikkansa eri lajeja. Kultaisesta leikkauksesta tai Fibonaccin luvuista ei ole mitään mainintaa.
Tutkijoiden kesken ei siis vallitse yksimielisyyttä siitä, käyttikö Bartók kultaista leikkausta ja Fibonaccin lukuja musiikkinsa rakenteellisella perustana. Kun hän itse ei ole lausunut asiasta mitään, kysymys jää puhtaasti spekulatiiviseksi. Sen sijaan näyttää siltä, että hänen musiikissaan ainakin jossakin määrin esiintyy kultaisen leikkauksen suhteita, vaikka kaikki metodisesti heikot ja kyseenalaisille laskutoimituksille perustuvat todistukset hylättäisiinkin. Tämän seikan merkitystä on kuitenkin pohdittu vähän tai ei ollenkaan. Ovatko kultaisen leikkauksen suhteet Bartókin musiikissa esteettisesti tärkeitä? Tälle kysymykselle on syytä omistaa enemmän huomiota.
Yhden painavan huomautuksen kultaisen leikkauksen suhteiden merkitystä vastaan on aivan ohimennen esittänyt E. Werner (1969, 514), joka kirjoittaa: ”Että esim. Bartók olisi tuntenut mieltymystä kultaista leikkausta ja sen suhteita kohtaan tosin kuulostaa hyvältä mutta selittää perin vähän, sillä sama voidaan pienellä vaivannäöllä osoittaa monista musiikin mestariteoksista.” Tämä huomautus luonnostelee historiallisen ja loogisen ongelman. Jos voidaan osoittaa, että kultaisen leikkauksen suhteita esiintyy monissa musiikin mestariteoksissa, niin silloin nämä suhteet eivät ole vain Bartókin musiikille tunnusomainen piirre, kuten Lendvai on pyrkinyt esittämään. Mitä yleisempiä kultaisen leikkauksen suhteet musiikissa ovat, sitä vähemmän niillä ylipäätään on merkitystä, sillä periaate, joka on niin yleinen että se kuvaa erotuksetta lähes kaikkea musiikkia, on tyhjä, sisällyksetön.
Wernerin väite, että kultaisen leikkauksen suhteita voidaan osoittaa monissa musiikin mestariteoksissa ansaitsee näin ollen huomiota. Jos se pitää paikkansa, Lendvain löydösten arvo vähenee, ja kysymystä kultaisen leikkauksen merkityksestä musiikissa on tarkasteltava laajemmassa yhteydessä.
Lütge
Willhem Lütge julkaisi v. 1936 artikkelin ‘Das architektonische Prinzip der Matthäuspassion J. S. Bachs’, jossa hänen päämääränään on osoittaa, että Matteus-passion rakennetta hallitsee niin pienissä yksityiskohdissa kuin suuressa muodossakin kultaisen leikkauksen periaate. Lütge viittaa aluksi barokin uskonnollis-filosofiseen maailmankuvaan, jonka hän olettaa olevan Bachin muotokielen taustana. Tuon aikakauden taiteilija tunsi uskonnolliseksi velvollisuudekseen jäsentää teoksensa samojen ankarien ja tarkoituksenmukaisten lakien mukaan, jotka hän hämmästyksen ja hartauden tuntein pani merkille koko luomakunnassa. Bachin aikalainen Andreas Werckmeister puki tämän periaatteen sanoiksi seuraavasti: ”Sopusuhtaisella ihmisellä on musiikilliset suhteet jäsenissään. Musiikki on näin ollen jumalan luomien kuvajainen, vieläpä itsekin jumalan kuva, koska se perustuu samaan muotoon ja suhteeseen kuin ihminen.” Zeisingille tämä lause olisi ollut kullan arvoinen, jos hän olisi sen tuntenut. Lütgen mukaan tämänkaltaiset ajatukset olivat Bachin aikakauden yhteistä omaisuutta, ja Bach oli kokonaan 18. vuosisadan lapsi. Emme tiedä eikä meidän ole tarpeenkaan tietää, Lütge huomauttaa, missä määrin Matteus-passion rakenteet perustuvat tietoisesti harkituille suhteille; Bach antoi joka tapauksessa ilmaisun sille, ”mitä tuolloin jokainen kantoi itsessään”.
Kultainen leikkaus, ”tuo kypsin ja esteettisesti tyydyttävin periaate”, toteutuu Lütgen mukaan useimmissa Matteus-passion aarioissa ja kuoroissa, jotka noudattavat joko italialaisen da capo -aarian tai saksalaisen Bar-muodon mallia. Ensimmäisen osan sopraanoaariassa ’Blute nur’ varsinainen aaria (A+B) käsittää 45 tahtia, joista A-osalle lankeaa 28 ja B-osalle 17 tahtia. Kun da capo -osa on A-osan tarkka kertaus, senkin kesto on 28 tahtia. Koko aarian suhteet 28 : 45 = 45 :73 (A:A+B = A+B:A+B+A) noudattavat vähäisen murto-osan poikkeamalla kultaista leikkausta, joka sitä paitsi ulottuu vielä B- ja A-osien suhteeseen (17:28 = 28:45). Paitsi muotoa kultainen leikkaus hallitsee laulettujen ja instrumentaalisten jaksojen suhdetta A-osassa (laulua 10 tahtia, soittimellisia jaksoja 18 tahtia eli 10:18 = 18:28). Toisena esimerkkinä Lütge analysoi toisen osan aarian ’Erbarme dich’, jossa kultaisen leikkauksen suhteet toteutuvat lähes samalla tarkkuudella.
Kuoro-osista kultaisen leikkauksen suhteita noudattaa selvimmin loppukuoro ’Wir setzen uns mit Tränen nieder’, jonka rakennetta Lütgen mukaan kuvaa parhaiten Lorenzin muotokäsite ’Reprisen-Bar’, vain sillä erotuksella että molemmat ’Stollenit’ kerrataan. Ensimmäinen ’Stollen’, käsittää 24 tahtia, toinen niin ikään 24 tahtia ja ’Abgesang’ 32 tahtia. Suhteet 80:48 = 48:32 vastaavat näin ollen likimain kultaista leikkausta, joka matemaattisen tarkasti olisi 80:49 = 49:31. Samalla tavalla varsinainen ’Bar’ suhtautuu molempiin kerrattuihin ’Stolleneihin’ (128:80 = 80:48). Täsmälleen samassa suhteessa ovat lopulta soittimelliset ja lauletut jaksot koko kuorossa. Moninaisia kultaisen leikkauksen suhteita Lütge löytää myös alkukuorosta ja koraalimuunnelmista ’O Mensch bewein dein Sünde gross’.
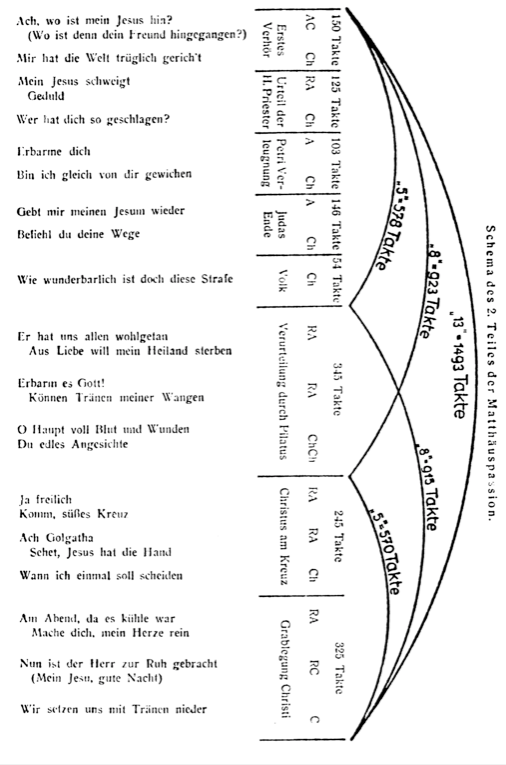
Tarkasteltuaan Matteus-passion yksittäisiä numeroita Lütge esittää kysymyksen, millaiset ”suurrytmiset lait” hallitsevat teoksen kokonaishahmoa. Tässä yhteydessä hän esittää varauksia siihen, miten perusteltua on käyttää tahteja laskennallisina yksikköinä, kun tarkastellaan suurmuotoa, ja mainitsee, että ainoa luotettava mittapuu on esityskesto. Vaikeutena on vain se, ettei Bach-tempoista vallitse mitään yhtenäistä käsitystä. Lütge on tiedostanut metodisen ongelman, mutta ei kykene sitä ratkaisemaan. Niinpä hän kiertää sen. Hän mainitsee tullessaan omissa tutkimuksissaan, joiden tuloksia hän ei kuitenkaan halua julkaista, siihen tulokseen, että kohtausten ja kohtausryhmien suhteet vastaavat täysin toisiaan laskettiinpa ne sitten tahtien lukumäärän tai esityskeston perusteella. Lepytettyään tällä tavoin tieteellistä omaatuntoaan Lütge ryhtyy laskemaan tahteja.
Tahtien lukumäärän mukaan laskettuna Matteus-passion toisen osan kultainen leikkaus sattuu tuomitsemis- ja ristiinnaulitsemiskohtausten rajalle (ks. Lütgen kaavio, kuva 5), tarkemmin sanottuna koraalisäkeistön ’Du edles Angesichte’ viimeiselle tahdille. Tässä koraalissa seurakunta kommentoi Kristuksen kuolemantuomiota. Käänteinen kultainen leikkaus puolestaan osuus koraalin ’Wie wunderbarlich ist doch diese Strafe’, jossa annetaan ilmaus seurakunnan tunteille Kristuksen kansalta saaman tuomion johdosta. Näiden pisteiden väliin jää toisen osan keskeinen kohtaus ’Pilatuksen tuomio’. Kohtausryhmien suhteet koko osassa vastaavat näin ollen likimain Fibonaccin lukuja 13:8:5:3, kuten Lütgen kaaviosta ilmenee. Bachilla näyttää siis olleen – Werckmeisterin sanoin ilmaistuna —”musiikilliset suhteet jäsenissään”, Lütge päättelee. ”Kenelläkään toisella ajan säveltäjällä ei ollut näin syvää, metafyysisesti juurtunutta muototajua kuin Bachilla. Niin monia Bachin aikalaisten teoksia kuin olen tutkinutkin, kenelläkään ei esiinny edes lähimain yhtä ankaraa, tiukkaa lainalaisuutta muodollisessa hahmottamisessa, ei enempää kultaisen leikkauksen kuin minkään muunkaan periaatteen mukaan.” Lütge näkee siis Bachin kuitenkin ainutlaatuisella poikkeuksena, vaikka toisaalta sanoo hänen olleen kokonaan aikansa lapsi ja antaneen ilmauksen sille, mitä jokainen kantoi itsessään. Ovatko siis Bach ja Bartók ne musiikinhistorian suuret arkkitehdit, jotka ovat löytäneet musiikillisen muodon plastisen kauneuden salaisuuden. Vai onko kultainen leikkaus musiikissa niin yleinen periaate, että se on riippumaton niistä historiallisista muutoksista, joita musiikin rakenteissa on tapahtunut?
Kuva 5
Kokkonen ja Webster
Joonas Kokkonen on, kuten tämän kirjoituksen alussa mainittiin, tutkinut Mozartin pianosonaattien rakennetta kultaisen leikkauksen kannalta. Sysäyksen tähän tutkimukseen antoi hänen sattumalta tekemänsä havainto, että kultaisen leikkauksen periaate hallitsee Mozartin B-duuri-sonaatin (K.V. 570) ensimmäisen osan rakenteita. Tässä sonaatissa käänteinen kultainen leikkaus (0.382 x 209 = 79.838) sattuu täsmälleen esittelyn ja kehittelyn rajalle ja kultainen leikkaus (0.618 x 209 = 129.162) varsin lähelle kehittelyn ja kertauksen rajakohtaa tahdissa 132. Kokkonen pitää tarkkuutta jälkimmäisessäkin tapauksessa hämmästyttävän suurena. ”Likiarvo riittää nimittäin hyvin kultaisen leikkauksen vaikutelman aikaansaamiseksi… Musiikissa muutaman tahdin poikkeamat eivät lainkaan hämärrä sectio aurean olemassaoloa.” Samat suhteet toteutuvat myös jaksojen sisäisessä rakenteessa. Esittelyjakson kultainen leikkaus sattuu tahtiin 49, jossa alkaa sivuteema tai sivuteeman tapainen taite, ja kehittelyn kultainen leikkaus osuu kohtaan, jossa pääteeman aiheet astuvat uudelleen esiin jne. Kokkonen toteaa, että tämän sonaatin ensimmäisen osan rakennetta kannattaa kokonainen kultaisen leikkauksen suhteiden verkosto, ja päättelee, että ”Sectio aurea -suhteita on niin paljon, ettei kysymys voi olla sattumasta”.
Tarkasteltuaan yksityiskohtaisesti ensimmäistä esimerkkiään Kokkonen esittää taulukkona laskemalla saadun kultaisen leikkauksen ja käänteisen kultaisen leikkauksen arvon kaikissa Mozartin pianosonaattien sonaattimuotoisissa osissa ja vertaa näin saatuja teoreettisia lukuja toisaalta kehittelyn ja kertauksen ja toisaalta esittelyn ja kehittelyn todellisiin rajakohtiin. Tuloksia hän kommentoi seuraavasti: ”Ensinnäkin huomataan, että laskemalla saadut rajakohtien tahtinumerot poikkeavat yllättävän vähän todellisuudessa esiintyvistä. Poikkeamat ovat suurimmillaan vähän toistakymmentä tahtia nopeissa osissa. Tällöinkin toinen kultaisen leikkauksen solmukohdista on jokseenkin kohdallaan (esim. K.V. 533, F, l: 91–102, 148–146) . Hitaan tempon huomioon ottaen suurimmat poikkeamat ovat epäilemättä F-duuri sonaatin K.V. 281 Andante amoroso -osassa (40–46, 65–59). Tämä poikkeus kuitenkin vain vahvistaa säännön: hyvin lyhyine ja mitättömine kehittelyineen ja muinekin piirteinen tämä osa vain kaukaisesti muistuttaa varsinaista sonaattimuotoista osaa.” Edelleen Kokkonen mainitsee pistokokein todenneensa, että myös jaksojen sisällä voidaan panna varsin laajalti merkille samantapaisia kultaisen leikkauksen suhteita kuin B-duuri-sonaatissa. ”Näin ollen voimme tehdä sen päätelmän, että Mozart ei ole kirjoittanut pianosonaateissaan ainoatakaan sonaattimuotoista osaa, josta sectio aurea puuttuisi. Päinvastoin kultainen leikkaus esiintyy useimmiten monena eri kerroksena rakennetta kannattaen.”
Kirjoittaessaan artikkeliaan Kokkonen ei näytä olleen tietoinen siitä, että hänen laskutoimituksensa oli jo aikaisemmin tehnyt J. H. Douglas Webster (1949), joka ilmoittaa analysoineensa kaikki Mozartin pianosonaatit ja todenneensa kultaisen leikkauksen useimmissa sonaattimuotoisissa osissa. Esimerkkinä Webster mainitsee C-duuri-sonaatin (K.V. 309) ensimmäisen osan, jonka 155 tahtia jakaantuvat seuraavasti (suluissa laskemalla saadut kultaisen leikkauksen arvot): kertaus t. 94 (96), esittelyn loppu t. 58 (59), toinen teema t. 35 (36), välike t. 21 (22). Kokkonen antaa vain kaksi ensimmäistä lukua. Kommentoidessaan poikkeamia Webster on sattumoisin kiinnittänyt huomiota samoihin seikkoihin kuin Kokkonen. Niinpä hän mainitsee, että F-duuri-sonaatissa (K.V. 533) vain pääjako (maior) on likimain kohdallaan; ja Kokkosen tavoin hänkin on laskenut c-molli-sonaatin (K.V. 457) ensimmäisen osan suhteet myös ilman koodaa ja huomauttaa, että tällöin pääjako on lähempänä ihannetta (mainitsematta kuitenkaan, että käänteinen kultainen leikkaus puolestaan on silloin siitä kauempana). Täysin eri mieltä Webster ja Kokkonen näyttävät olevan vain Es-duuri-sonaatin (K.V. 282) ensiosasta: Websterin mukaan se on kahdenpuolinen eikä osoita kultaisen leikkauksen häivääkään, kun taas Kokkonen on saanut sille likimain ihanteelliset arvot.
Mozartin pianosonaattien kohdalla kaksi eri tutkijaa on – ilmeisesti toisistaan riippumatta – päätynyt pitkälle yhtäpitäviin tuloksiin. Havaintojen paikkansapitävyyttä ei siis juuri kannata epäillä.
Mozartin pianosonaattien lisäksi Webster on käynyt läpi vaikuttavan määrän muuta musiikkia ja tullut siihen tulokseen, että kultaisen leikkauksen suhde on tyypillinen sonaattimuodolle ylipäätään ja että se myös rajoittuu melkein yksinomaan tähän muotoon, vaikka saattaakin olla osittain läsnä myös muissa muodoissa. Esitän tässä suppean läpileikkauksen Websterin laajasta esimerkkiaineistosta. Mozartin kymmenestä viimeisestä jousikvartetosta kahdeksassa kertausjakson alku osuu likimain kultaisen leikkauksen kohdalle. Beethovenin pianosonaatit perustuvat kultaiselle leikkaukselle yhtä selvästi kuin Mozartin. Sama pätee seuraavien sinfonioiden ensiosiin, kun koodaa ei oteta huomioon: I, V, VII, VIII ja IX (toinen puolisko). Myös toisen sinfonian ensiosa noudattaa kultaista leikkausta, jos johdanto jätetään pois laskuista. Edelleen tämä suhde esiintyy selvänä Beethovenin seitsemässätoista jousikvartetossa, joista Webster esittää malliesimerkkinä c-molli-kvarteton (op. 18 nro 4) ensiosan (kuva 6):

Kuva 6
Samankaltaisia suhteita saadaan, kun lasketaan tahteja eteenpäin kultaisesta leikkauksesta tai lopusta alkuun. Koko osan rakenne on näin ollen terassimainen tai sillan kaltainen: kaaret pitenevät rakennetta kultaisen leikkauksen molempien jakojen kohdalla kannattavien pilareiden suuntaan ja lyhenevät niiden jälkeen.
Myös Haydnin jousikvartetoissa on useita esimerkkejä kultaisesta leikkauksesta; parhaisiin kuuluu d-molli-kvarteton op. 1 nro 3 ensiosa, jonka rakenteelliset rajakohdat noudattavat melkein täsmälleen Fibonaccin lukusarjaa: 88, 57, 34, 21, 13, 8 (teoreettisesti 88, 55, 34, 21, 13, 8). Sinfonioista riittävään tarkuuteen yltää ainakin nro 104 d-molli (ensimmäinen osa). Brahmsin sinfonioiden alkuosissa poikkeamat ovat myös varsin vähäisiä. Schubertin h-molli-sinfoniassa samaa periaatetta toteuttaa ensimmäisen osan ohella myös toinen. Muita esimerkkejä Schubertilla ovat jousikvartetot op. 29 a ja op. posth. d, nokturno op. 148 es ja laulu Gretchen am Spinnrade, jossa huippukohta ”dein Kuss” osuu kultaiseen leikkaukseen. Mendelssohnilla tätä suhdetta tavataan sanattomassa lauluissa, Chopinilla nokturnoissa (esim. op. 9 nro 2 Es ja op. 48 nro 1 c), Schumannilla pianokvintetossa, Tshaikovskilla viidennessä sinfoniassa, Dvorákilla sellokonsertossa, Skrjabinilla Poème de l’extasessa, Debussylla orkesteriteoksissa Nuages ja La Mer, Schönbergillä jousikvartetoissa II–IV, Bartókilla toisessa viulukonsertossa sekä jousikvartetoissa V ja VI jne.
Websterin luettelo ei jätä epäilyksille sijaa: kultaisen laikkauksen suhde on sangen yleinen sonaattimuodon rakennemallia noudattavissa sävellyksissä tai sävellysten osissa. Kokkonen mainitseekin, että kultaisen leikkauksen suhde syntyy ”kuin itsestään”, jos kehittely on ”oikein mitoitettu”. Kokkonen on myös sitä mieltä, etteivät muutaman tahdin poikkeamat lainkaan hämärrä sectio aurean olemassaoloa.
Lopuksi
Onko meidän pidettävä todistettuna, että kultainen leikkaus on yleinen ja merkitsevä rakenneperiaate länsimaisessa musiikissa? Voidaksemme esittää perustellun arvion tästä kysymyksestä meidän on tarkasteltava tutkimuksessa käytettyä metodia.
Kultaisen leikkauksen teoreetikot ovat yleensä mitanneet musiikkia käyttämällä laskennallisena yksikkönä joko tahtia tai pienintä sävellyksessä esiintyvää aika-arvoa. Näin on menetellyt myös Lütge (1936, 75), joka periaatteessa kuitenkin on sillä kannalla, että ainakin laajoja kokonaisuuksia tarkasteltaessa ainoa luotettava mittapuu on esityskesto. Menettelyään hän on puolustanut sillä, että ainakin Bachin musiikissa kokonaisuuden osille saadaan samat suhteet kummallakin tavalla laskettuna. Myös Webster (1949, 242) on ilmaissut samantapaisen käsityksen: ”Sävelteoksia tulisi tietenkin arvioida etupäässä korvakuulolta ajassa: mutta monet testit osoittavat, että ajassa mittaaminen ja silmän avulla tehty tahtianalyysi tuottavat samassa sävellyksessä lähes vastaavan tuloksen.” Webster lienee kuitenkin sekoittanut korvakuulolta arvioimisen ja keston mittaamisen, sillä esimerkeissään hän mainitsee kestoja sellaisella tarkkuudella, että ne on voitu saada vain mittaamalla.
Näille kahdelle menetelmälle, kestojen mittaamiselle ja tahtien tai aika-arvojen laskemiselle partituurissa, on yhteistä, että ne ovat tietyssä mielessä ”objektiivisia”: kuka tahansa voi toistaa operaation ja tarkistaa tuloksen. Toisaalta ne eroavat siinä suhteessa, että niiden kohteena on eri objekti. Jos mitataan esityskestoa, kohteena on – Ingardenin kielellä sanottuna – ”reaalinen objekti”, joka on ajassa; jos taas lasketaan tahteja tai aika-arvoja, kohteena on ”puhtaasti intentionaalinen objekti”, jolla on aika itsessään. Näin ollen Jalas (1955) ja Kauko (1981), jotka kumpikin ovat analysoineet Sibeliuksen viidettä sinfoniaa, puhuvat eri asioista. Kuitenkin molemmat ovat löytäneet kohteestaan kultaisen leikkauksen suhteita.
Jalaksen lähtökohtana ovat sinfonian osien väliset ja sisäiset kestosuhteet hänen omissa esityksissään. Hän tutkii näin ollen oikeastaan omaa käsitystään teoksessa vallitsevista suhteista. Kun tämä käsitys on yksityistapaus monien muiden tulkintojen joukossa, sen ei voida sanoa ainakaan yksin edustavan käsitettä Sibeliuksen viides sinfonia. Tästä huolimatta Jalaksen tulokset ansaitsevat huomiota. Hän on esittänyt ne havainnollisen kaavakuvan avulla (kuva 7), josta ilmenee, että käänteinen kultainenleikkaus sattuu ensimmäisessä osassa esittelyn ja kehittelyn rajalle, että toinen ja kolmas osa noudattavat likimain samoja suhteita ja että kokonaisuus, joka alkaa ensimmäisen osan kehittelyjakson alusta ja päättyy finaalin allegron loppuun, jakaantuu myös samassa suhteessa niin, että rajakohtana on ensimmäisen ja toisen osan välinen tauko. Tällä tavoin muodostuu sekä perättäisiä että osittain päällekkäisiä suhteita, jotka likimain noudattavat Fibonaccin lukuja 3:5:8 ja 5:8:13.
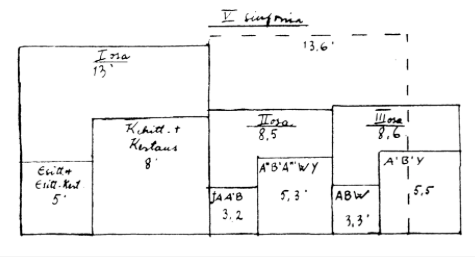
Kuva 7
Kaukon tarkastelun kohteena on Sibeliuksen viidennen sinfonian ensimmäisen pariosan, varsinkin sen alkupuoliskon rakenne sellaisena kuin se ilmenee partituuria lukevalle tarkastelijalle. Aluksi Kauko esittää tavanomaisesta poikkeavan tulkinnan siitä, missä ensimmäisen osan pääteema ja sitä seuraava transitio päättyvät, ja saa tulokseksi, että ”transition ja pääteman kestojen suhde [on] tuhannesosan tarkkuudella kultainen leikkaus eli 1.618”. Tuhannesosan tarkkuuden tavoittelu on saanut Kaukon pohtimaan myös kysymystä, kuuluuko ”esim. johdannon lopun fermaatista osa pääteemaan” ja päätymään ehdotukseen, että fermaattikin olisi jaettava kultaisen leikkauksen suhteessa, jolloin ”voimme kokea myös itse johdannon jakautuvan noin sadasosan tarkkuudella […] kultaisen leikkauksen mukaisesti”.
Hämmentävää tässä analyysissa on ensinnäkin se, että Kauko puhuu kultaisen leikkauksen kokemisesta, kun hänen metodiset edellytyksensä riittävät korkeintaan sen laskemiseen. Toiseksi laskutoimituksissa saatu hämmästyttävä tarkkuus herättää epäilyn, että ensin on laskettu määrätyn kokonaisuuden kultainen leikkaus ja sen jälkeen etsitty musiikillisia perusteita sille, että juuri sillä kohden on pääteeman ja transition raja. Rajakohdan todellinen kriteeri on tällöin kultainen leikkaus, eivät musiikkianalyyttiset argumentit, joiden funktio on lähinnä dekoratiivinen.
Amerikkalainen tutkija Eric Werner on huomauttanut: ”Että esimerkiksi Bartók olisi tuntenut mieltymystä kultaista leikkausta ja sen suhteita kohtaan tosin kuulostaa hyvältä, mutta selittää perin vähän, sillä sama voidaan pienellä vaivannäöllä osoittaa monista musiikin mestariteoksista.” Jo edellä esitetyn aineiston perusteella on ilmeistä, että Werner on oikeassa. Jos periaate kuitenkin on niin yleinen, että se sopii melkein kaikkeen musiikkiin, se on myös sisällyksetön. Sitä voidaan pitää analyyttisesti yleisenä eli tautologisena totuutena, joka on sinänsä pätevä mutta joka ei kerro todellisuudesta mitään. Mikä tahansa kokonaisuushan voidaan aina jakaa kultaisen leikkauksen suhteessa. Tämän jälkeen ei tarvita enää muuta kuin hiukan analyyttista mielikuvitusta sen selittämiseksi, miksi kultaisen leikkauksen tuleekin olla juuri siinä mihin se lankeaa. Harjaantunut analyytikko löytää aina enemmän tai vähemmän päteviä argumentteja sille, että leikkaus sattuu johonkin myös puhtaasti musiikillisin perustein merkittävään rajakohtaan.
Yhtä ilmeistä on, että musiikin rakenteissa ilmenee monia muitakin matemaattisia suhteita. Niiden ympärille ei kuitenkaan ole versonnut perinnettä, joka olisi verrattavissa kultaisesta leikkauksesta käytyyn keskusteluun. Tämä saattaa johtua Fibonaccin lukujen poikkeuksellisen mielenkiintoisista matemaattisista ominaisuuksista, jotka ovat omiaan kiehtomaan lukumystiikkaan taipuvaista mieltä. Onhan kultaisen leikkauksen havaittu toteutuvan mitä moninaisimmissa luonnon ja elämän ilmiöissä auringonpilkkujen ja Niilin tulvien kausivaihteluista arvopapereiden ja huonekalujen tuotannon suhdannekiertoon.
Kun on ymmärretty, että kultaisen leikkauksen esiintymisen todistaminen musiikissa on turhaa, koska se voidaan aina löytää, on palattava vielä kysymykseen tämän suhteen mahdollisesta esteettisestä merkityksestä. Kultaisen leikkauksen teoreetikkojen tavallisin vastaus on teesi, että tämä suhde koetaan harmonisena ja miellyttävänä tai johdonmukaisena ja ”oikeana”, vaikka sitä ei sellaisenaan havaittaisikaan. Bachmann ja Bachmann (1979, 81–82) muotoilevat teesin seuraavasti: ”Ilmeisesti kukaan Bartókin musiikkia kuunteleva henkilö ei tule tietoiseksi näistä suhteista, vaikka hän todennäköisesti voi saada vaikutelman musiikissa vallitsevasta tasapainosta. Kouliintunutkaan muusikko ei kykene tunnistamaan Fibonaccin tai kultaisen leikkauksen suhteita soivasta musiikista. Mutta tasapainon vaikutelma musiikin suhteissa on helpommin tunnistettavissa; se antaa hänen musiikilleen ’rauhoittavamman sävyn’ siinä mielessä, että kuulija kokee lyhyempien ja pitempien rakenteellisten muodostelmien välisen tasapainon suhteet ’täydellisinä’.” Lowman (1971, 537), on samalla kannalla: ”Tuleeko kuulija tietoiseksi ’Fibonacci-suhteista’ niiden vilahtaessa ohi? Todennäköisesti ei, mutta tästä huolimatta ne kuitenkin täyttävät tehtävänsä. Kuulija saa vaikutelman tasapainosta, tunteen että hänen kuulemansa musiikilliset tapahtumat ovat ’oikeilla’ paikoilla, että ne muodostavat mieltä kiinnittäviä aikarakenteita.” Kramer (1973, 118) puolestaan pitää tietyin edellytyksin mahdollisena jopa kuulla Fibonacci-suhteita (puhumattakaan Kaukosta, joka kertoo tuhannesosan tarkkuudella koetuista ”täsmällisistä aikaelämyksistä”). Kramer mainitsee Bartókin Allegro barbaron ostinato-tahtiryhmät, joiden kestosuhteiden havaitseminen on hänen mielestään mahdollista sen tähden, että nämä tahdit ovat musiikin sisällön kannalta täysin eriytymättömiä ja staattisia: niissä on vain yksi ainoa sointu. Empiiriset havainnot eivät kuitenkaan tue tätä käsitystä. Somfai (1981, 261), joka totesi tahtien lukumäärän eroavan Bartókin äänityksessä ja nuoteissa, mainitsee, ettei tämän eron havaitseminen ole mahdollista, jos äänite soitetaan oikeassa tempossa; laskeminen tulee mahdolliseksi vasta, kun nopeus vähennetään puoleen.
Somfain havainto vie meidät suoraan asian ytimeen. Kun kultaisen leikkauksen teoreetikot ovat laskeneet tahteja ja aika-arvoja tai esityskestoja, heidän tarkastelunsa kohteena on ollut sävelteos intentionaalisena tai reaalisena objektina. He ovat kuitenkin tehneet sen johtopäätöksen, että samat suhteet vallitsevat myös sävelteoksessa fenomenaalisena, havaittuna objektina, joka muodostuu kuulijan tajunnassa. Tälle loogiselle hyppäykselle ei ole perusteita; sitä vastaan puhuu kaikki, mitä tiedämme musiikillisen ajan hahmottamisesta.
Venäläinen psykologi Beljajeva-Exempljarskaja teki jo 1920-luvulla kokeita, joissa koehenkilöitä pyydettiin arvioimaan kolmen Skrjabinin preludin kestoa. Virheitä osattiin odottaa, mutta sittenkin oli yllättävää, että hyvin monet koehenkilöt erehtyivät arviossaan monta sataa prosenttia suuntaan tai toiseen. Subjektiivisen ajankokemuksen suuret vaihtelut ovat olleet yleisesti tunnettuja jo kauan, ja monet filosofit ovat pohtineet niiden syitä. Esim. William James mainitsee, että vaihtelevia ja mielenkiintoisia kokemuksia sisältävä ajanjakso tuntuu lyhyeltä kuluessaan mutta pitkältä jälkeenpäin muisteltuna, tapahtumaköyhä ajanjakso taas pitkältä kuluessaan mutta lyhyeltä jälkeenpäin. Hänen ajatustaan on erityisesti musiikin kokemisen osalta kehitellyt edelleen Henry F. Orlov (1979), joka mainitsee mm. että kuulijan mahdollisuus havaita kestosuhteet oikein on suurimmillaan silloin, kun hän on vähiten kiinnostunut kuulemastaan ja pienimmillään silloin, kun hän kokee voimakkaan musiikillisen elämyksen. Jos tämä käsitys on oikea, niin silloin on ristiriitaista ajatella, että todellisessa musiikillisessa objektissa esiintyvät kultaisen leikkauksen suhteet perustelisivat sen esteettisen arvokokemuksen, joka muodostuu havaitussa objektissa. Kultaisen leikkauksen teoreetikot näyttävät kokonaan sivuuttaneen musiikillisen taideteoksen ajallisen luonteen, vaikka puhuvatkin kestosuhteista, ja tarkastelevat sävellystä abstraktina spatiaalisena mielikuvana, jossa rakenteellisia suhteita voidaan mitata ja arvioida samalla tavalla kuin käyttöesineissä ja kuvataiteen teoksissa.
Luonnontieteiden menettelytavoista, laskemisesta ja mittaamisesta, näyttää tulleen joillekin musiikin tutkijoille tiedonhankinnan ihanne. Tämän ilmiön syyt ovat ymmärrettävät. Sen taustana on epäilemättä ikivanha uskomus siihen, että musiikki ja matematiikka ovat läheistä sukua toisilleen ja että musiikki, scientia quae de numeris loquitur, kuten keskiajan oppineet sitä nimittivät, heijastaa pienoiskoossa maailmankaikkeuden ikuisia lainalaisuuksia. Kultaisen leikkauksen myytissä näyttävät heränneen henkiin uusplatonilaisuuden opit. Siitä uneksivien musiikinteoreetikkojen mielessä väikkyy ja kangastelee mielikuva hyvinjärjestetystä taiteesta, jossa vallitsee sopusuhta ja harmonia. Löytäessään etsimänsä matemaattisen suhteen sävelteoksesta he uskovat selvittäneensä sen suuruuden salaisuuden, ylistävät säveltäjän neroutta ja tuntevat kenties antiikin filosofien tavoin itsekin samastuvansa siihen harmoniaan, joka on heidän tarkastelunsa kohteena. Mutta ehkäpä on oikeutettua nähdä heidän ajattelussaan myös epävarmuutta ja turvallisuuden kaipuuta, erottaa salainen toive varman perustan löytämisestä taiteen arvoille maailmassa, jossa esteettiset normit näyttävät yksi toisensa jälkeen osoittautuvan epävarmoiksi ja petollisiksi. Historismin ja esteettisen relativismin hyökkäykset taiteen mestariteosten arvovaltaa ja sen esteettisiä perusteita vastaan ovat pakottaneet etsimään uudelleen jo kerran löydettyä mutta sittemmin unohtunutta ja kadotettua viisautta.
Kirjallisuutta
Bachmann T. & P.J. Bachmann 1979. An Analysis of Béla Bartók’s Music through Fibonaccian Numbers and the Golden Mean. The Musical Quarterly 65, 72–82.
Beardsley, Monroe C. 1958. Aesthetics. Problems in the Philosophy of Criticism. New York.
Birkhoff, George D. 1933. Aesthetic measure, Cambridge, MA.
Chailley, J. 1966. Essai d’analyse du Mandarin Merveilleux. Studia Musicologica 8, 11–39.
Fechner, Gustav Theodor 1876. Vorschule der Ästhetik. Leipzig.
Herz-Fischler, R. 1994. Fibonacci and the “Fibonacci sequence”. The Golden Number, and Division in Extreme and Mean Ratio. Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences II, toim. I. Grattan-Guinness. London, 1579–1584.
Jalas, Jussi 1955. Sibeliuksen sinfoniat ja “kultainen leikkaus”. Uusi Musiikkilehti 2:9, 17–19.
Kauko, Olavi 1981. Sibelius ja aika. Kuvastimessa …durch einen Spiegel… Joonas Kokkonen, toim. Timo Mäkinen ym., Savonlinna, 129–135.
Kokkonen, Joonas 1976. Mozartin pianosonaatit ja sectio aurea. Juhlakirja Erik Tawaststjernalle 10.X.1976 (Acta Musicologica Fennica 9), toim. E. Salmenhaara. Keuruu: Otava, 101-107.
Kramer, Jonathan 1973. The Fibonacci Series in Twentieth-Century Music. Journal of Music Theory 17.
Kuokkala, Pekka 1978. Sectio aurea Joonas Kokkosen oopperassa Viimeiset kiusaukset. Lisensiaatintyö. Jyväskylän yliopiston musiikkitieteen laitos.
Lendvai, Ernö 1957. Einführung in die Formen- und Harmonienwelt Bartóks. Béla Bartók. Weg und Werk, Schriften und Briefe, toim. B. Szabolcsi. Budapest: Corvina, 91–137.
— 1960. Bartók und die Zahl. Melos 27, 327–331.
— 1971. Béla Bartók. An Analysis of his Music, London.
— 1983. The Workshop of Bartók and Kodály. Budapest: Editio Musica.
— 1993. Symmetries of Music. Kecskemét: Kodály Institute.
Lipps, Theodor 1914. Grundlegung der Ästhetik, 2.p. Leipzig & Hamburg.
Lowman, Edward 1971. Some Striking Proportions in the Music of Béla Bartók. The Fibonacci Quarterly 9, 527–528 ja 536–537.
Lütge, Wilhelm 1936. Das architektonische Prinzip der Matthäuspassion J. S. Bachs. Zeitschrift für Ästhetik und allgemeine Kunstwissenschaft 30, 65–80.
Orlov, Henry F. 1979. The Temporal Dimensions of Musical Experience. The Musical Quarterly 65, 368–378.
Petersen, Peter 1971. Die Tonalität im Instrumentalschaffen von Béla Bartók. Hamburg.
Pfrogner, Hermann 1963. Hat Diatonik Zukunft? Musica 17, 146–155.
Somfai, László 1981. Die “Allegro barbaro” -Aufnahme von Bartók textkritisch bewertet. Documenta Bartókiana 6, toim. L. Somfai. Budapest: Akadémiai Kiadó, 259–275.
Szentkirályi, András 1978. Some Aspects of Béla Bartók’s Compositional Techniques. Studia Musicologica 20, 157–182.
Tatarkiewicz, Wladislaw 1970. History of Aesthetics I. Warszawa.
Webster, J.H. Douglas 1949. Golden Mean Form in Music. Music & Letters 30, 238-248.
Werner, E. 1969. Grundsätzliche Betrachtungen über Symmetrie in der Musik des Westens. Studia Musicologica 11, 487–515.
Zeising, A. 1854. Neue Lehre von den Proportionen des menschlichen Körpers. Leipzig.
Musiikki 12 (1982), 247–292. Päivitetty 2020.